Circular Ack Vector Buffer implementation notes

Implementation Notes: Circular Ack Vector Buffer

This memo describes particulars of implementing the circular buffer described in Appendix A of RFC 4340.

1. Buffer fields

The buffer is implemented as an array of size ARRSIZ with two indices, head and tail. Both range from 0...ARRSIZ-1.

In addition the buffer has an overflow flag to indicate if and when the buffer has overflowed. A larger buffer will not be allocated on overflow, to keep the implementation simple. If necessary, it can later be extended, e.g. by signalling overflow state to the peer (e.g. using a SyncAck with a Slow Receiver option).

When the buffer has overflowed, its length is equal to ARRSIZ. Under normal conditions, it is defined as the number of elements from head to tail. Since the buffer pointers move from right to left, the buffer length is computed as modulo-ARRSIZ subtraction of head from tail:

		buf_len  =  (tail + ARRSIZ - head) % ARRSIZ
			 
			     +-- 	
			     |   tail - head 		    if head <= tail
			 =  < 
			     |   ARRSIZ - (head - tail)    if head  > tail
			     +--

This formula can be verified on the examples to follow.

2. Buffer states

This section illustrates the buffer behaviour with ARRSIZ=4. The `h' and `t' arrows indicate the positions of the head and tail pointers, respectively.

2.1 Initialisation

The buffer is empty when head == tail. It does not matter where the pointers are initially positioned.

2.2 Filling up the buffer

Both pointers move from right to left, i.e. from higher to lower array indices. When reaching the lowest index (0), the pointers wrap around to start at the rightmost index (ARRSIZ-1) again. Manipulation of the head/tail pointers is done using a macro,

advance_ptr(p)  =  ((p) + ARRSIZ - 1) % ARRSIZ

For instance, with ARRSIZ=4, when head=0 then advance_ptr(head) results in head=3; when head=2 then advance_ptr(head) gives 1; and so on.

2.2.1 First insertions up to overflow

First round of insertions up to the overflow of the circular buffer

The maximum buffer fill level is reached when the tail/head pointers are immediately adjacent (third picture); at this time it contains ARRSIZ-1 elements. Applying the buf_len formula from above,

in the first picture we have buf_len = (0 + 4 - 3) % 4 = 1,
in the third picture we get buf_len = (0 + 4 - 1) % 4 = 3.

In the last picture however, buf_len equals 0. This is because the overflow is indistinguishable from the empty condition. Therefore, to distinguish overflow from empty buffer state, an `overflow' flag is used, so that tail == head means that the buffer is

empty whenever overflow == 0,
full beyond capacity (buf_len == ARRAYSIZ) whenever overflow == 1.

Under normal operational conditions, tail != head, overflow == 0, and 0 <= buf_len <= ARRAYSIZ-1.

2.2.2 First wrap-around

In all examples below overflow == 1. Old entries are overwritten, and the tail and head pointers move in lock-step.

Overwriting old entries with new ones when the buffer is overflown

Overwriting old entries with new ones when the buffer is overflown

The possibility of overflow introduces another problem:

If it can be ensured that the buffer never overflows (e.g. through generous overprovisioning) then the buffer requires no locks to synchronise access: the head pointer is only moved by the insertion routine, and the tail pointer is only moved when acknowledgments come in.

The pointers in overflowed state and the overflow flag, however, are manipulated by both routines and require a mutual-exclusion mechanism, to avoid that that two different routines try to advance the tail pointer (or clear the overflow flag) at the same time.

2.3 Freeing space in the buffer

Buffer space is freed by advancing the tail pointer (in the same direction as the head pointer) when new acknowledgments come in. Again the handling is different if the buffer overflowed; illustrated in the next two subsections.

2.3.1 Acking old packets in a non-overflowed buffer

We use this full buffer as starting point.

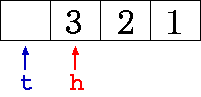
The following images show the states after acking 1, 2, and 3, respectively; gradually emptying the buffer.

Acknowledging old packets in a non-overflowed buffer

2.3.2 Acking old packets in an overflowed buffer

In addition to moving the tail pointer as above, the overflow flag needs to be cleared when acknowledging old packets in an overflowed buffer. As starting point we use the following, the state shortly before the second wrap-around.

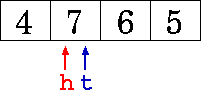
The succession of images below illustrate acking 4, 5, 6, and 7. In the last figure, the buffer is again empty.

Acknowledging old packets when the buffer previously overflowed

3. Test program

From the above observations, a simple test program can be derived. A runnable example is here.