Ack Vector processing at the HC-receiver  

This text summarises particularities of the Linux DCCP Ack Vector implementation.

1. Assumptions

  1. The tail pointer always points to the first unused cell after the live portion of the buffer (illustrated here). This simplifies handling the overflow case and computing the length. The price is that (in a non-overflowed buffer) one cell is wasted; but it will be used when the buffer overflows.

  2. When reserving space for packets which have not yet been received, the `holes' in the sequence space are allocated as one entry each per sequence number (each having state 3 and a run length of 0), as suggested in the first part of RFC 4340, A.1.1. Multiple missing packets will not fill a single entry with a non-zero run length, since this introduces complexity of reshuffling a possibly large buffer and handling the involved cases (e.g. when runlength exceeds 63).

  3. No buffer compression is performed. The main reason is that it adds computational and algorithmic complexity; in particular with regard to updating the Acknowledgment Window (RFC 4340, 11.4.2), since the old position of ack_ptr may no longer be valid and thus becomes unreliable.

2. Updating the Acknowledgment Window

This section describes how to update the buffer state at the HC-receiver when the HC-sender acknowledges receipt of Ack Vectors that the HC-receiver sent previously. This is related to section A.3, "Clearing State", of RFC 4340. The first step is to locate the corresponding Ack Vector record.

2.1 Finding the right record and updating the list

In the Linux implementation, Ack Vector records are successively added at the head of the list, so that the most recent record is always at the top. When searching for older records, the list is traversed from tail to head (i.e., oldest entries first), and records are found using the following test on each record in the list (assuming that the ack number on the HC-sender packet is `ackno' ):
A test program which verifies these tests on sample sequence numbers can be found here.

2.2 Updating the buffer state

After the receiver has successfully located the right Ack Vector Record, we have the following information:
ack_ptr:
The value of buf_head at the time of sending the Ack Vector.
ack_ackno:
The acknowledgment number on which the Ack Vector was based.
ack_runlen:
Then run length of the buffer at position `ack_ptr' at the time of sending the Ack Vector.
We use the following variables to refer to the current buffer state:
ptr:
Position in buffer corresponding to ack_ptr.
ptr_ackno:
Acknowledgment number associated with ptr (not necessarily the same as ack_ackno).
ptr_runlen:
Run length of the buffer at position `ptr'.
When considering the conditions which could lead to ptr != ack_ptr, the above assumptions (which ensure that ptr == ack_ptr) are now justified:  if we perform buffer compression, then ptr may well be different from ack_ptr, so that we would have to recompute the correct buffer position.

There are now three possible cases:
  1. ptr_runlen == ack_runlen
    This implies ptr_ackno == ack_ackno and is dealt with by setting buf_tail = ptr (illustrated here).

  2. ptr_runlen < ack_runlen
    This case implies a bug: since we don't do buffer compression, the run length can only grow, but not shrink, over time.

  3. ptr_runlen > ack_runlen
    In this case, further packets have arrived after the Ack Vector was sent. It implies ptr_ackno > ack_ackno and is described in the following diagram, where the horizontal cells denote consecutive sequence numbers (and not buffer cells).
Computing a new run length when packets have arrived after sending the Ack Vector

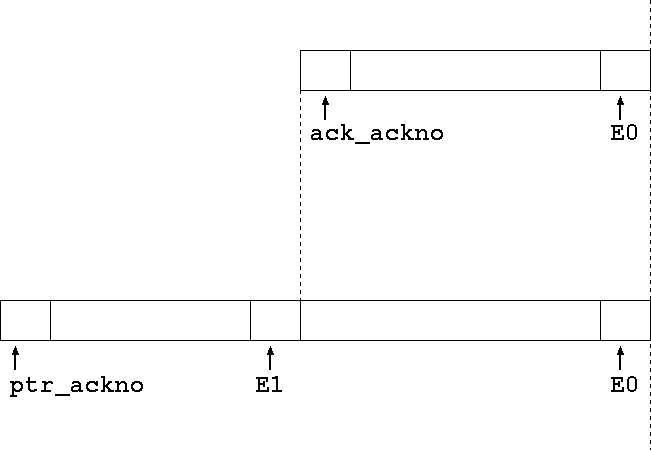
The acknowledgment by the HC-sender is up to and including ack_ackno. Both Ack Vector cells cover down to  E0, which is given as 
		E0 = ack_ackno - ack_runlen = ptr_ackno - ptr_runlen.			(NB: all addition/subtraction here is modulo-48).
We need to find the new lower end E1 and the corresponding new run length:
		ptr_runlen'  =  ptr_ackno - E1
Since E1 = ack_ackno + 1, we have ptr_runlen' = ptr_ackno - ack_ackno - 1, i.e.
		ptr_runlen'  =  (E0 + ptr_runlen) - (E0 + ack_runlen) - 1
			     =  ptr_runlen - (ack_runlen + 1),
which gives the new run length to be entered in the buffer cell at ack_ptr. Since (ptr_runlen' + 1) packets are still unacknowledged by the sender, we advance buf_tail to the cell preceding ack_ptr (thus clearing state for all packets with sequence number older than E0).

3. Handling overflow

The circular buffer is statically allocated to match reasonable operational conditions, so that overflow appears as exception case. The following section discusses the chosen recovery strategy for overflow.

3.1 Existing alternatives

 In RFC 4340, section A.1.1 the following alternatives are suggested:
The existing Linux implementation uses the second alternative (drop-on-overflow).

3.2 Discussion and choice of other alternative

There is a third alternative - treating overflow as special case. In this case the head/tail pointers move in lock-step, as described here. The difference between the second and the third scheme is:
From the user perspective, continue-on-overflow is less disturbing: the HC-receiver continues to pass on data to the user and continues to send Ack Vectors. This strategy is useful when for instance an outstanding Ack from the HC-sender is just delayed or re-ordered. The drop-on-overflow strategy, in contrast, applies the ostrich principle and will disrupt user data flow.

Both have in common that ultimately packets will be considered lost by the HC-sender:
  • In the case of drop-on-overflow, no new Ack Vectors will be generated until an Ack for the older data (which may long have been lost) arrives; in the worst case this leads to complete stand-still.
  • Continue-on-overflow, on the other hand, will in the worst case let the sender consider some old packets as lost, while newer packets continue to be acknowledged. In the best case, continue-on-overflow `gets away with' a transient overflow where all data from the sender is acknowledged.
Due to the above stated advantages, continue-on-overflow has been chosen as strategy for dealing with overflow.

The first alternative (buffer compression) is not considered, as it has two main disadvantages. First, it is expensive to perform and brings no guarantee that the compression will free enough space. The second disadvantage is that it complicates the process of matching Ack Vector records with buffer cells  -  when buffer compression is used, ack_ptr becomes useless and positions need to be recomputed from scratch, whereas otherwise the value of ack_ptr can be used directly.

3.3 Short description of overflow handling

The receiver tracks the overflow condition by setting an overflow bit. As long as overflow prevails, the head and tail pointers move in lock-step, thereby erasing older data. To avoid ambiguities (caused by older acknowledgments from the sender), the receiver only keeps the most recent Ack Vector record in its list. If this is acknowledged, the entire buffer is acked and so reverts to the empty state. Otherwise, the overflow condition continues - visible via repeated warnings in the system log.

4. Computing ECN nonces

When using a buffer larger than the room consumed by a single Ack Vector (253 bytes), keeping track of the ECN nonce is a problem, since the Ack  Vector nonce is relative to the length of the Ack Vector, but not relative to the length of the buffer.

The solution is straightforward: the buffer is allocated in N units of 253 bytes and there is an array buf_nonce[N] of nonce sums, where buf_nonce[i] is the nonce sum of buffer cells (i-1) * 253 up to i * 253, for i > 1. The ack_nonce then contains the one-bit parity sum of all elements in buf_nonce that cover live parts of the buffer.